Spacial Orientation for Developers in a Hurry

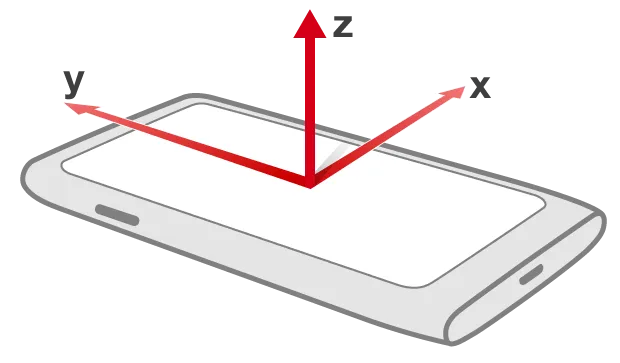
So you’d like to respond programmatically to changes in the spacial orientation of a mobile device. Perhaps you’re writing a feature that directs the user towards a nearby location, or you’d just like to add some surprise and delight parallax to your loading screen.

You might expect the Android OS to send you gyro sensor readings as a set of “Euler Angles”: yaw, pitch, and roll. It doesn’t.

If you don’t typically use 3d graphics APIs and you’d like an intuitive justification for why the Android OS instead gives you a quaternion, read on.

The goal is not to re-hash the math-heavy tutorials you find everywhere online. Rather, we’ll see why 3d applications and frameworks ( Unity3d , OpenGL , and countless more) use quaternions. We’ll end with a practical example of translating a quaternion into the familiar Euler angles.

Euler Angles

Oh yeah, before we start I want to be clear about yaw, pitch, and roll.

You might be sitting in something like this:

Spin around like you’re trying to make yourself dizzy. That’s your yaw.

Now rock back and forth like you’re on the porch drinking a lemonade. That’s your pitch.

Now fall over on your side (but don’t hurt yourself). That’s your roll.

The combination of these angles can express whatever direction you’re facing in an easy to visualize format, and for simple use cases these angles express everything you need to know. However, there are some mathematical (and engineering) pitfalls. Problems arise when trying to combine orientations, or interpolate an orientation change from a starting to resting position.

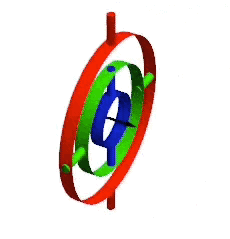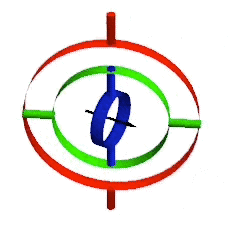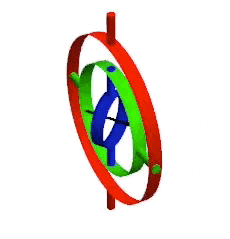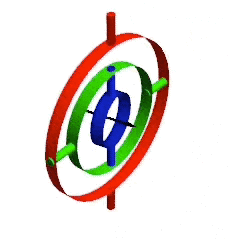
You might even be familiar with one such problem, called gimbal lock: two axes of rotation align closely enough that rotations of their common plane are lost. These boundary conditions are not just an artifact of engineering a physical gyroscope. They arise in the math, where smooth gradations turn to jagged spikes, making it difficult to interpret the combination of many distinct rotations.

Quaternions are a different way to express rotations in 3d space that are easier to combine and interpolate, making them a sensible choice for 3d computing.

Quaternions

Quaternions express rotations, but how do they get past the awkward boundary conditions we saw above? I won’t bother re-stating what 3Blue1Brown already beautifully demonstrated in video form — if you’re even slightly curious how to visualize the 3d rotations, I highly recommend that video. For now, we won’t need that level of detail to appreciate the trick quaternions are pulling. We can stay in 2d.

There’s something simpler that you’ve seen before (pre-calc!), and allows pulling an analogous trick.

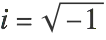
On its face, the square root of negative one seems like a mathematical black hole. But as we know it gave rise to the complex numbers, where (among other things) an exploitable property was discovered: rotations on the complex plane can be expressed as a multiplication by i. When you multiply complex numbers, you add their angles.

Like complex numbers, quaternions have special rules governing their addition, subtraction, multiplication, and division. What previously involved traditional trigonometry (like a rotation) can instead be expressed arithmetically with quaternions.

This article assumes you’re in a hurry, but check out the additional links at the end if you’d like a deeper dive (with the guidance of some experts!).

You’ve pacified my curiosity for now, how about an example?

To start getting spacial rotation data from the Android OS, register a listener with the SensorManager for Sensor.TYPE_ROTATION_VECTOR. You’ll need a Context:

Your listener can react to those sensor readings. If you’d like to convert the rotation vector to a set of Euler angles, there’s a couple helper methods right on SensorManager itself:

The incoming event.values array is the quaternion, and the helper methods are there to assist transforming into the more elemental yaw/pitch/roll format.

You can view the full gist here .

More about quaternions:

• Collin Flynn

  Principal Software Engineer

  More from Collin